Stages/2010-10-04/Groupe3 - Site des stages Hippocampe de l’IREM d’Aix-Marseille

Définition axiomatique de la caractéristique

Poster

- Les fondamentaux des axiomes de χ On considère : χ(-)= 1 et χ(--)= 2 , en prenant " - " est un segment . Mais pour χ(O)? ( Le O étant un cercle ) χ(A∪B)= χ(A)+ χ(B)- χ(A∩B)= 1 + 1 - 2 = 0 ( voir schéma ) Et pour χ(∞) ? χ(A)= 0 et χ(B)= 0 et χ(A∩B)= -1 . Donc χ(∞)= -1 . ( voir schéma ) Prenons un autre exemple , celui d'un début de collier . ( voir schéma ) Puisque χ(O O)= 0 , χ(-)= 1 et χ(> <)= -2 , alors d'après le second axiome : χ(A∪B)= χ(A) + χ(B)- χ(A∩B)= 0 + 1 - 2 = -1 .

- Problème de récurrence

Le calcul établi lors du paragraphe ci-dessus peut-il s'appliquer pour n éléments ?

Grâce au principe de récurrence et aux axiomes nous pouvons établir pour n objets A1, A2,..., A(N) la relation suivante où χ désigne khi : χ(A1 U A2 U...U A(N)) = χ(A1)+ χ(A2) +...+ χ(A(N)).

Intéressons-nous maintenant à la caractéristique d'Euler sur les colliers : -(désigne un segment), O (désigne un cercle), }{ (désigne les intersections entre cercles et segments).

Le collier se présente sous la forme notée C : O}-{O}-{...}-{O}-{O avec n cercles qui est composé de cercles notés A : O O O ... O O O n cercles disjoints où grâce aux axiomes χ(A)=0, de segments disjoints notés B : - - - ... - - - n-1 segments où χ(B)=n-1, d'intersections A∩B : { } { } { } ... { } { } { } 2(n-1) intersections où χ(A∩B)=2(n-1).

χ(C)=χ(A∪B) donc χ(A∪B)=χ(A)+χ(B) χ(A∩B)=0+n-1-(2(n-1))=1-n

- Colliers & Courbes En ce qui concerne les Colliers et les Courbes nous avons pu voir qu'à partir de figures composées de cercle et de trait ( segments ) , nous pouvons retrouver une structure de la forme d'un collier et ainsi pouvoir calculer la caractéristique de χ ( Khi ) toujours à partir de l'axiome : χ(A∪B)= χ(A)+ χ(B)- χ(A∩B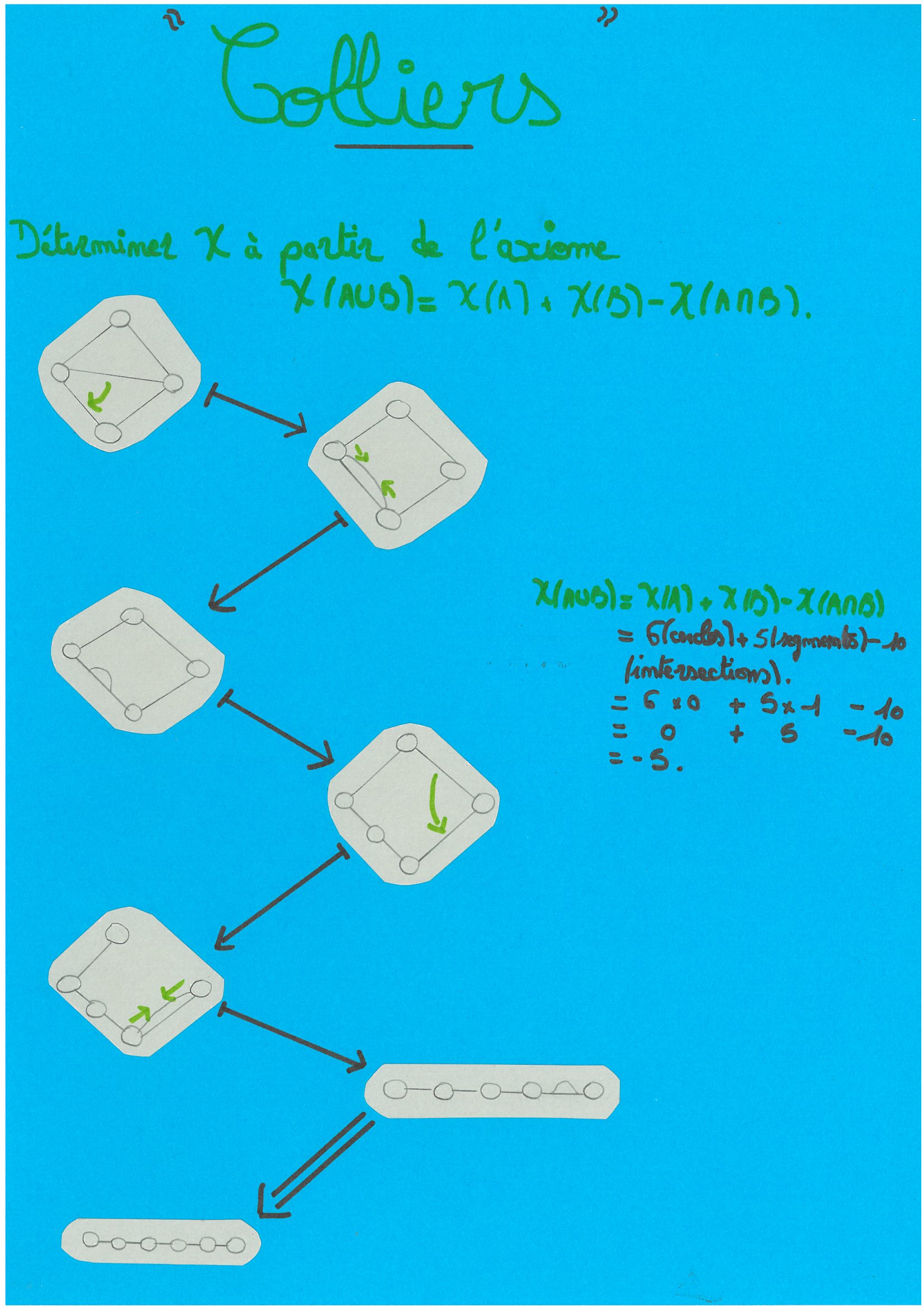). Sur cette image , on peut constater que si l'on fait glisser les traits sur les cercles , on finit par former ce que l'on appelle une structure collier . Il est par contre important de préciser que l'on ne doit absolument pas déchirer ou casser quelque chose lorsque l'on modifie la structure de la figure ( faire glisser les éléments entre eux ne casse pas la liaison qu'ils entretiennent ). Ayant au final , une structure "collier" , nous pouvons maintenant calculer la caractéristique de χ en considérant que : A correspond aux cercles , B correspond aux traits et (A∩B) correspond aux intersections . Nous pouvons donc dire que : χ(A∪B) = χ(A)+χ(B)-χ(A∩B) χ(A∪B) = 6 (cercles) + 5 (segments) - 10 (intersections)= 6x0 + 5x1 - 10 = -5 Puisque χ(cercle)= 0 et χ(segment)= 1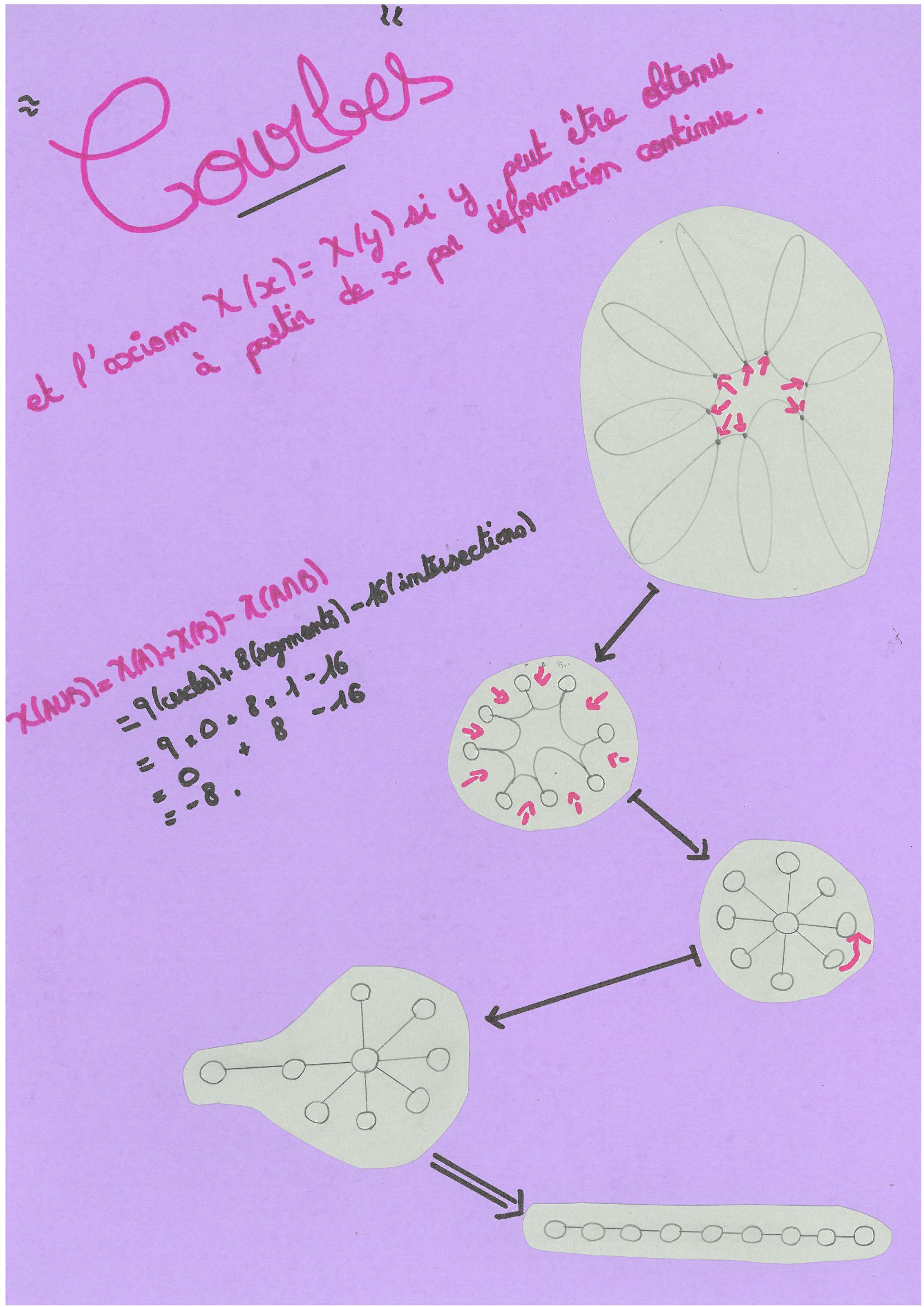. Cette figure reprend le même procédé en partant simplement d'une structure , d'une forme de départ différente.

Hippocampe: Stages/2010-10-04/Groupe3 (dernière édition le 2015-09-11 13:15:30 par LionelVaux)